Elementos de la circunferencia 

Secantes, cuerdas y tangentes.

Existen varios puntos, rectas y segmentos, singulares en la circunferencia:

• centro, el punto interior equidistante de todos los puntos de la circunferencia;
• radio, el segmento que une el centro con un punto de la circunferencia;
• diámetro, el mayor segmento que une dos puntos de la circunferencia, y lógicamente, pasa por el centro;
• cuerda, el segmento que une dos puntos de la circunferencia; las cuerdas de longitud máxima son los diámetros;
• recta secante, la que corta a la circunferencia en dos puntos;
• recta tangente, la que toca a la circunferencia en un sólo punto;
• punto de tangencia, el de contacto de la tangente con la circunferencia;
• arco, segmento curvilíneo de puntos pertenecientes a la circunferencia;
• semicircunferencia, cada uno de los dos arcos delimitados por los extremos de un diámetro.

La circunferencia y un punto: posiciones relativas 

Un punto en el plano puede ser:

• Exterior a la circunferencia, si la distancia del centro al punto es mayor que la longitud del radio.
• Perteneciente la circunferencia, si la distancia del centro al punto es igual a la longitud del radio.
• Interior a la circunferencia, si la distancia del centro al punto es menor a la longitud del radio.

La circunferencia y la recta: posiciones relativas [editar]

Una recta, respecto de una circunferencia, puede ser:

• Exterior, si no tienen ningún punto en común con ella y la distancia del centro a la recta es mayor que la longitud del radio.

• Tangente, si la toca en un punto (el punto de tangencia) y la distancia del centro a la recta es igual a la longitud del radio. Una recta tangente a una circunferencia es perpendicular al radio que une el punto de tangencia con el centro.

• Secante, si tiene dos puntos comunes, es decir, si la corta en dos puntos distintos y la distancia del centro a la recta es menor a la longitud del radio.

Relación entre dos circunferencias: posiciones relativas [editar]

Dos circunferencias, en función de sus posiciones relativas, se denominan:

• Exteriores, si no tienen puntos comunes y la distancia que hay entre sus centros es mayor que la suma de sus radios. No importa que tengan igual o distinto radio. (Figura 1)

• Tangentes exteriormente, si tienen un punto común y todos los demás puntos de una son exteriores a la otra. La distancia que hay entre sus centros es igual a la suma de sus radios. No importa que tengan igual o distinto radio. (Figura 2)

• Secantes, si se cortan en dos puntos distintos y la distancia entre sus centros es menor a la suma de sus radios. No importa que tengan igual o distinto radio. Dos circunferencias distintas no pueden cortarse en más de dos puntos. Dos circunferencias son secantes ortogonalmentesi el ángulo entre sus tangentes en los dos puntos de contacto es recto. (Figura 3)

• Tangentes interiormente, si tienen un punto común y todos los demás puntos de una de ellas son interiores a la otra exclusivamente. La distancia que hay entre sus centros es igual a la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra. (Figura 4)

• Interiores excéntricas, si no tienen ningún punto común y la distancia entre sus centros es mayor que 0 y menor que la diferencia de sus radios. Una de ellas tiene que tener mayor radio que la otra.

• Interiores concéntricas, si tienen el mismo centro (la distancia entre sus centros es 0) y distinto radio. Forman una figura conocida como corona circular o anillo. Una de ellas tiene que tener mayor radio que la otra. (Figura 5)

• Coincidentes, si tienen el mismo centro y el mismo radio. Si dos circunferencias se cortan en más de dos puntos, necesariamente son circunferencias coincidentes.

Ángulos respecto de una circunferencia [editar]

Ángulos en la circunferencia.

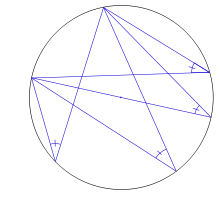
Arco capaz: los cuatro ángulos inscritos determinan el mismo arco y por tanto son iguales.

Un ángulo, respecto de una circunferencia, pueden ser:

Ángulo central, si tiene su vértice en el centro de ésta. Sus lados contienen a dos radios.

La amplitud de un ángulo central es igual a la del arco que abarca.

Ángulo inscrito, si su vértice es un punto de la circunferencia y sus lados contienen dos cuerdas.

La amplitud de un ángulo inscrito en una circunferencia equivale a la mitad del ángulo central que delimita dicho arco. (Véase: arco capaz.)

Ángulo semi-inscrito, si su vértice es un punto de la circunferencia y sus lados contienen una cuerda y una recta tangente a la circunferencia. El vértice es el punto de tangencia.

La amplitud de un ángulo semi-inscrito es la mitad de la del arco que abarca.

Ángulo interior, si su vértice está en el interior de la circunferencia.

La amplitud de un ángulo interior es la mitad de la suma de dos medidas: la del arco que abarcan sus lados más la del arco que abarcan sus prolongaciones.

Ángulo exterior, si tiene su vértice en el exterior de ésta.

La amplitud de un ángulo exterior es la mitad de la diferencia de los dos arcos que abarcan sus lados sobre dicha circunferencia.

Longitud de la circunferencia 

La longitud  de una circunferencia es:

donde  es la longitud del radio.

Pues  (número pi), por definición, es el cociente entre la longitud de la circunferencia y el diámetro: