Centros del triángulo

Geométricamente se pueden definir varios centros en un triángulo:

• Baricentro: es el punto que se encuentra en la intersección de las medianas, y equivale al centro de gravedad
• Circuncentro: es el centro de la circunferencia circunscrita, aquella que pasa por los tres vérticesdel triángulo. Se encuentra en la intersección de las mediatrices de los lados. Además, la circunferencia circunscrita contiene los puntos de intersección de la mediatriz de cada lado con las bisectrices que pasan por el vértice opuesto.
• Incentro: es el centro de la circunferencia inscrita, aquella que es tangente a los lados del triángulo. Se encuentra en la intersección de las bisectrices de los ángulos.
• Ortocentro: es el punto que se encuentra en la intersección de las alturas.
• Exincentros: son los centros de las circunferencias exinscritas, aquellas que son tangentes a loslados del triángulo. Se encuentra en la intersección de una bisectriz interior y dos bisectricesexteriores de los ángulos.

El único caso en que los cuatro primeros centros coinciden en un único punto es en un triángulo equilátero.

Cálculo de elementos en un triángulo

Para resolver triángulos utilizamos generalmente el Teorema de Pitágoras cuando son triángulos rectángulos, o los Teoremas del seno y del coseno.

Elementos notables de un triángulo

Medianas y centro de gravedad

Medianas y centro de gravedad de un triángulo

Se lama mediana de un triángulo cada una de las tres líneas que pasan por un vértice del triángulo y por el punto medio del lado opuesto al vértice.

Cada una de las tres medianas dividen el triángulo en dos triángulos de áreas iguales.

Las tres medianas de un triángulo son concurrentes. Su punto de intersección G es llamado centro de gravedaddel triángulo.

Mediatrices y círculo circunscrito

Mediatrices y círculo circunscrito de un triángulo.

Se llama mediatriz de un triángulo a cada una de lasmediatrices de sus lados [AB], [AC] et [BC].

Las tres mediatrices de un triángulo son concurrentes en un punto Ω equidistante de los tres vértices. El círculo de centro Ω y radio ΩA que pasa por cada uno de los tres vértices del triángulo es el círculo circunscrito al triángulo.

Notas:

• Un triángulo es obtusángulo si y sólo si las bisectrices se cortan fuera del triángulo.
• Un triángulo es acutángulo si y sólo si las bisectrices se cortan dentro del triángulo.

Propiedad:

• ABC es un triángulo rectángulo en A si y sólo si el centro de su círculo circunscrito es el centro de [BC].

Bisectriz y círculo inscrito

Bisectrices y círculo inscrito de un triángulo.

Las bisectrices de un triángulo son las tres bisectrizesde sus ángulos internos.

Las tres bisectrices de un triángulo son concurrentes en un punto O. El círculo inscrito del triángulo es el único círculo tangente a los tres lados del triángulo y está totalmente incluido en el triángulo. Tiene por punto central O, que es pues el centro del círculo inscritoen el triángulo.

Alturas y ortocentro

Alturas y ortocentro de un triángulo

Se llama altura de un triángulo a cada una de las tres líneas que pasan por un vértice del triángulo y son perpendiculares a la cara opuesta al vértice. La intersección de la altura y el lado opuesto se denomina «pie» de la altura.

Estas 3 alturas se cortan en un punto único H llamadoortocentro del triángulo.

Notas:

• Un triángulo es rectángulo si y sólo si su ortocentro es uno de los vértices del triángulo
• Un triángulo es obtusángulo si y sólo si su ortocentro se encuentra fuera del triángulo
• Un triángulo es acutángulo si y sólo si su ortocentro está dentro del triángulo

Recta y círculo de Euler

Recta y círculo de Euler de un triángulo.

Los tres puntos H, G y Ω están alineados en una línea recta llamada recta de Euler del triángulo y verifica la relación de Euler:

Por otra parte, los puntos medios de los tres lados, los tres pies de las alturas y los puntos medios de los segmentos [AH], [BH] y [CH] están en un mismo círculo llamado círculo de Euler o círculo de los nueve puntos del triángulo.

En el espacio

Octaedro; poliedrode ocho caras triángulares.

Icosaedro; poliedro de veinte caras triangulares

El triángulo es la forma de las caras de muchospoliedros regulares:tetraedro (cuatro caras que son triángulos equiláteros, es la pirámide de base triangular),octaedro (ocho caras, las pirámides de Egipto son medio-octaedros), icosaedro (veinte caras) ...

Historia

Problemas R49-> R55 del papiro Rhind.

Ningún documento matemático del Antiguo Imperio ha llegado hasta nosotros. Pero la arquitectura monumental de la (III Dinastía y la IV Dinastía de Egipto es una prueba notable de que los egipcios de esa época tenían conocimientos relativamente sofisticados de geometría, especialmente en el estudio de los triángulos.

Figura del triángulo representada en el problema R51 del papiro Rhind

El cálculo de la superficie de esta figura se analiza en los problemas R51 del papiro Rhind, M4, M7 y M17 del papiro de Moscú, que datan todos del Imperio Medio. El problema R51 constituye en la historia mundial de las matemáticas, el primer testimonio escrito que trata del cálculo de la superficie de un triángulo.

Enunciado del problema R51 del papiro Rhind

²

El término mryt significa probablemente la altura o el lado. Sin embargo, la fórmula utilizada para calcular el área hace pensar en la interpretación en favor de la primera solución.³ El escriba tomaba la mitad de la base del triángulo y calculaba el área del rectángulo formado por ese lado y la altura; es decir

equivalente a la fórmula general utilizada en nuestros días:

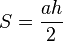
El hecho de que un triángulo de lados 3-4-5 es rectángulo también era conocido por los antiguos egipcios y mesopotámicos.

Euclides, en el Libro I de sus Elementos , hacia el 300 antes de Cristo, enunció la propiedad de la suma de los ángulos del triángulo.