la geometria - ecuaciones de la circunferencia

Ecuaciones de la circunferencia

Ecuación en coordenadas cartesianas

En un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el punto (a, b) y radio r consta de todos los puntos (x, y) que satisfacen la ecuación

$(x-a)^2 + (y-b)^2 = r^2,$ .

Cuando el centro está en el origen (0, 0), la ecuación anterior se simplifica al

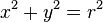$x^2 + y^2 = r^2,$ .

La circunferencia con centro en el origen y de radio la unidad, es llamada circunferencia goniométrica, circunferencia unidad o circunferencia unitaria.

De la ecuación general de una circunferencia,

$(x-a)^2 + (y-b)^2=r^2 ,$

se deduce:

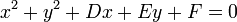
$x^2+y^2+Dx+Ey+F=0 ,$

resultando:

$a = frac{-D}{2}$

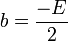
$b = frac{-E}{2}$

$r = sqrt{a^2 + b^2-F}$

Si conocemos los puntos extremos de un diámetro: $(x_1,y_1), (x_2,y_2),$ ,

la ecuación de la circunferencia es:

$(x-x_1)(x-x_2)+(y-y_1)(y-y_2)=0.,$

Ecuación vectorial de la circunferencia

Sin información

Ecuación en coordenadas polares

Cuando la circunferencia tiene centro en el origen y el radio es c, se describe en coordenadas polares como $(r,theta) ,$

$r=c. ,$

Cuando el centro no está en el origen, sino en el punto 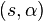$(s,alpha) ,$ y el radio es $c ,$ , la ecuación se transforma en:

$r^2 - 2 s r, cos(theta - alpha) + s^2 = c^2$

Ecuación en coordenadas paramétricas [editar]

La circunferencia con centro en (a, b) y radio c se parametriza con funciones trigonométricas como:

$x=a + c cos t, y=b+csin t,qquad tin[0,2pi]$

y con funciones racionales como

$x=a+cleft(frac{1-t^2}{1+t^2}right), y=b+cleft(frac{2t}{1+t^2}right),qquad -inftyleq tleq infty$

Área del círculo delimitado por una circunferencia

El área del círculo delimitado por la circunferencia es:

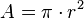
$A = pi cdot r^2$

Esta última fórmula se deduce sabiendo que el área de cualquier polígono regular es igual al producto del apotema por el perímetro del polígono dividido entre 2, es decir: 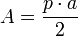$A = frac{p cdot a}{2}$ .

Considerando la circunferencia como el caso límite de un polígono regular de infinitos lados, entonces, el apotema coincide con el radio, y el perímetro con la longitud de la circunferencia, por tanto:

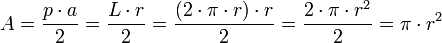
$A = frac{p cdot a}{2} = frac{L cdot r}{2} = frac{(2 cdot pi cdot r) cdot r}{2} = frac{2 cdot pi cdot r^2}{2} = pi cdot r^2$

Otras propiedades

Triángulos rectángulos inscritos en una semicircunferencia.

El segundo teorema de Tales muestra que si los tres vértices de un triángulo están sobre una circunferencia dada, siendo uno de sus lados el diámetro de la circunferencia, entonces, el ángulo opuesto a éste lado es un ángulo recto (véase arco capaz).

Dados tres puntos cualesquiera no alineados, existe una única circunferencia que contiene a estos tres puntos (esta circunferencia estará circunscrita al triángulo definido por estos puntos). Dados tres puntos no alineados en el plano cartesiano 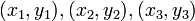$(x_1,y_1), (x_2,y_2), (x_3,y_3) ,$ , la ecuación de la circunferencia está dada de forma simple por la determinante matricial:

$detbegin{bmatrix} x & y & x^2 + y^2 & 1 x_1 & y_1 & x_1^2 + y_1^2 & 1 x_2 & y_2 & x_2^2 + y_2^2 & 1 x_3 & y_3 & x_3^2 + y_3^2 & 1 end{bmatrix} = 0.$